『波』と聞くと、海岸に打ち寄せては引く波を思い浮かべる人が多いでしょう。
しかし、この世界にはたくさんの波があります。例えば、
音波(声、音楽、騒音など)、電磁波(電波など)、水面波、地震波、重力波 …
波とは、”いったりきたり”、つまり振動です。振動には様々なものがあります。例えば、
上-下、左-右、前-後、高-低、大-小、強-弱、濃-淡、明-暗 …
・打ち寄せる波は、岸から見れば [前-後] に振動しています。
・雨が水たまりに作る波は、水面が [上-下] に振動しています。
・音は、空気の濃い部分と薄い部分が振動して伝わります。
波には、縦波と横波があります。
【縦波】波が進む方向と同じ方向に振動する波 … 音波がそれです。
【横波】波が進む方向と90度の角度で振動する波 … 水面波がそれです。
地震波には、縦波(P波)と横波(S波)があります。P波は縦波ですが、進行方向と同じ方向に振動する揺れのことであり、上下に揺れる縦揺れのことではないので間違えないでください。
P波とS波の関係は、
・伝わる速さ :P波 > S波
・揺れる大きさ:P波 < S波
この性質を利用したものが「緊急地震速報」です。早く伝わってくるP波をとらえることで、その後に襲ってくる大きなS波に備えるための仕組みです。ですので、震源地に近い所では緊急地震速報が間に合わないので役に立ちません。
生物の世界にも波が存在します。例えば、シマウマ、キリン、ヒョウ、トラなど動物の模様は、実は「チューリングの方程式」という波の式で表すことができます。この方程式のパラメーターを変えることで、縞模様やヒョウ柄やまだら模様などを自在に作ることができます。
物理学においても波は重要な分野です。弦を弾いたときの振動や、電磁波・量子の性質に至るまで、すべて「波動方程式」という式で表すことができます。これは非常に難しい学問なので専門家以外の人たちには縁がないと思います。しかし、波動方程式は知らなくても、波に関する次の現象は誰もが経験しているはずです。
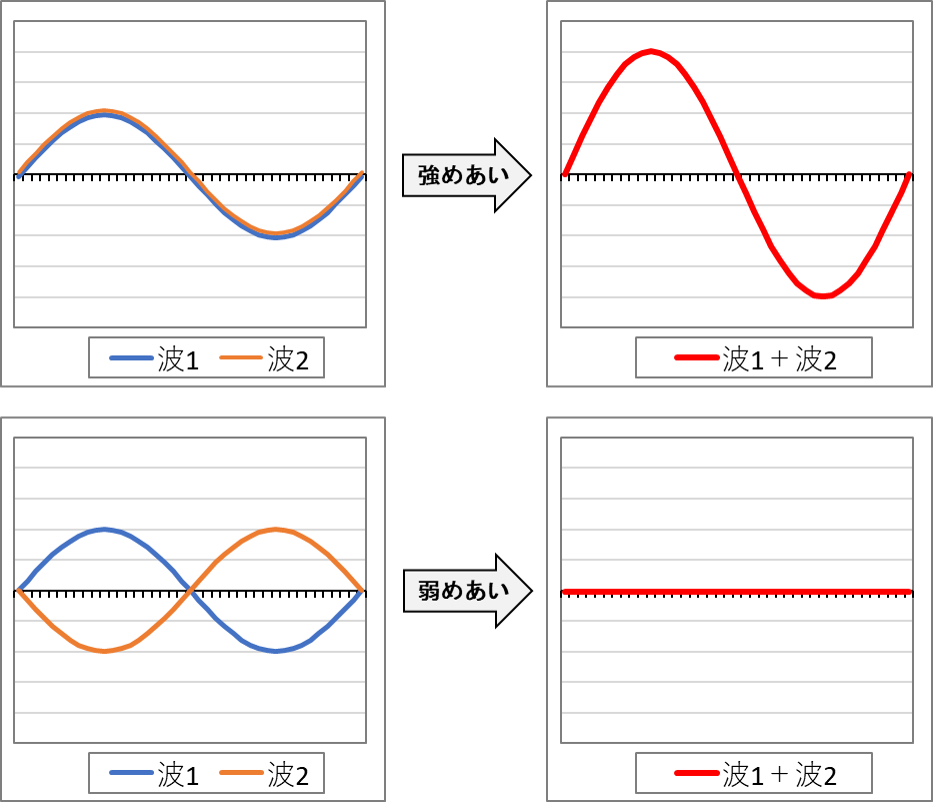
それは「波の干渉」です。簡単に言うと、複数の波が重なったときの「強めあい」と「弱めあい」です。
・高い波同士や低い波同士が重なると、揺れが大きくなります。これが波の「強めあい」です。
・高い波と低い波が重なると、相殺されて揺れが小さくなります。これが波の「弱めあい」です。
音楽を聴くときににノイズキャンセリング機能付きヘッドホンを使ったことがある人も多いのではないでしょうか。周囲の雑音を小さくすることができるので便利ですね。実は、このノイズキャンセリング機能も、波の干渉(弱めあい)の原理を用いた仕組みです。雑音は空気の波ですから、その波と逆の形の波(音)を強制的に作ることによって雑音を相殺させて打ち消しているのです。
台風や嵐のとき、風によって作られた近くの波と遠くで作られた波(うねり)が重なって、突然大きな波(高波)が起きることがあります。また、津波が入り江に入ると、岸に反射した複数の波が重なって干渉(強めあい)を起こし、普通の海岸線よりも波が高くなります。
波は、波長(一回りする長さ)、振幅(揺れ幅)、位相(開始位置)によって様々な形があります。それらの異なった形の波を重ね合わせると、とても複雑な波になります。
次のグラフは、波1、波2、波3を重ね合わせた結果です。このように、たった3つの単純な波でも、重ね合わせると複雑な動きになります。
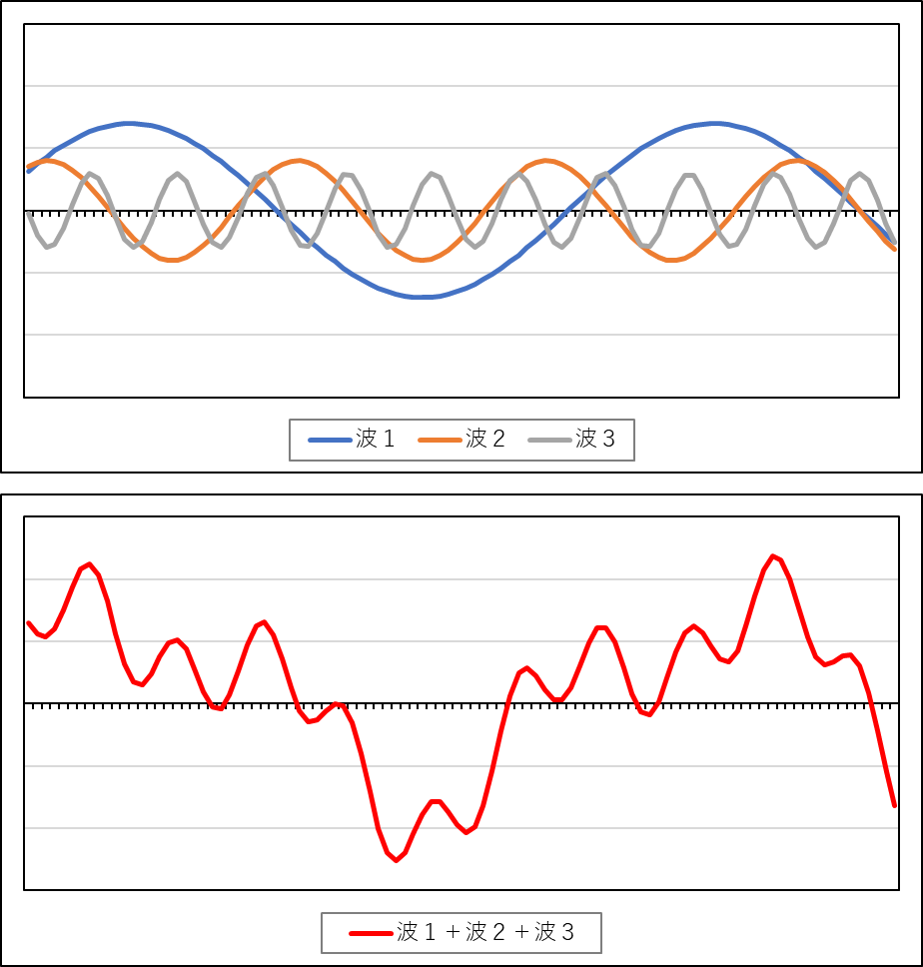
逆に言うと、一見複雑な動きでも、分解すると単純な波の重ね合わせであることがあります。この、”複雑な動きを、単純な波の重ね合わせで表現する” ための解析法があります。とても難しい学問ですが、興味がある方は『フーリエ解析』を勉強してみてください。
フーリエ解析は、工学系や物理・数学系の大学で詳しく学ぶ “とても難しい学問” なので、それ以外の人は手が出せないかも知れません。しかし、その根本的な考え方は「QC7つ道具」で学ぶ【層別】と同じです。
【層別】とは、集まったデータを解析する際に、特定の条件によってデータを分類してから分析することです。異なる条件のデータが混在していると、傾向や因果関係が見えにくくなります。そのようなときは、層別に分析することで見えやすくなることがあります。例えば、工場別、装置別、年代別などです。
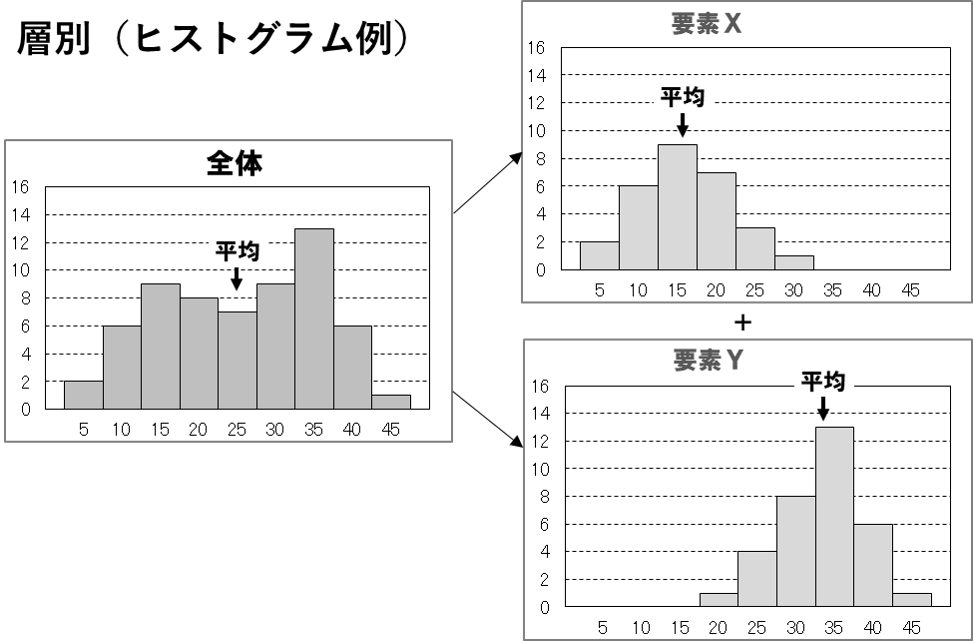
層別はその時点で集まっているデータ群が対象ですが、波の解析は “その時点” ではなく “推移” なので、分析に必要な次元として [時間軸] が追加されます。そのため当然難しくなりますが、「複雑なことは分けて考える」という点はどちらも同じです。
何か問題があって分析しても傾向や原因が分からないとき、集まったデータを層別に分けて分析すると共に、問題が発生するタイミングに波がないか(複数の周期性の重ね合わせだと考えられないか)を考えてみるのもよいかも知れません。

コメント